Celestial Navigation – Artificial Horizon_b – Telecommunications, Navigation & Electronics

Introduction

Fig.1 Sextant Bubble Horizon & MagLite with Red Lens for Night Vision

In a recent post I looked at adapting an artificial bubble horizon to my sextant using a 3D printed bracket. I calibrated the combination with a water horizon on Lake Ontario (Ref.1). In this post I look at taking measurements of the Moon altitude on Sept12th & Oct5th using the artificial horizon from my home location. Figure 1 shows the unit with a red lens maglite for taking measurements without losing night vision.

Measurement

Fig.2 View Sextant Telescope Showing Moon & Bubble & Alignment Target Circles

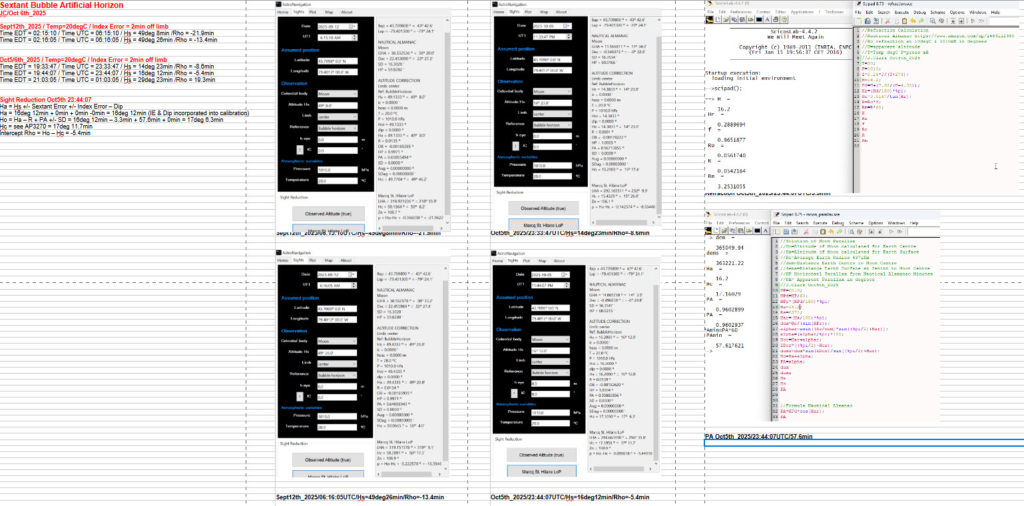
Figure 2 shows the view of the moon through the sextant telescope and the alignment target circles & bubble. Taking measurements requires a lot of patience and practice. The bubble must be located precisely in the inner target circle. The sextant has to be moved laterally to do this as well as rotated so that the unit is perfectly vertical and horizontal. Then the micrometer can be adjusted to move the moon image directly into the bubble centre. Finally the moon is in the centre of the bubble which is in the centre of the inner target circle and all axes lines are aligned.

Figure 3 shows a spreadsheet with the two measurements on Sept 12th and three on Oct 5th. I used NavAlgos to calculate the intercept error the best being -5.4min on Oct 5th. As I mentioned in the previous post the printed bracket may have some play due to it being plastic vs. metal.

Sight Reduction Oct 5th

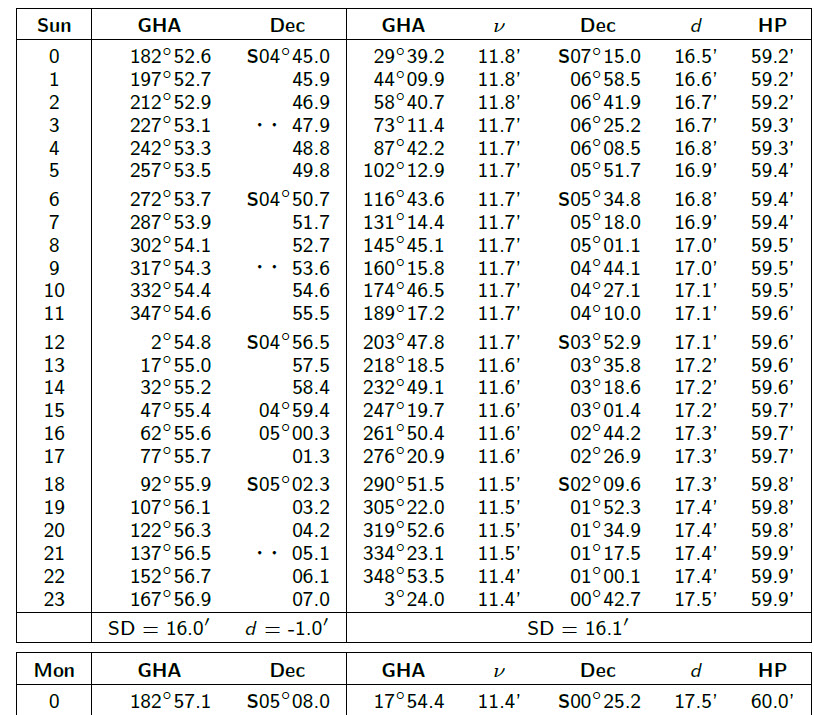
In order to reduce the sight and calculate the intercept Rho, we first have to determine the Moon GP for Oct5th_2025 at 23:44:07UTC. Figure 4 shows the Nautical Almanac for the Sun & Moon (2nd column) for Oct 5th_2025:

delGHA_moon23/24hrs=(17deg54.4min-3deg24min)=14deg30.4min
delTime=(44min7sec/60min)=0.7352778
delGHA_moon23/sighting=14deg30.4min * 0.7352778=10deg40min
GHAmoon/sighting=14deg4min
delDEC_moon23/24=0deg42.7minS – 0deg25.2minS=-17.5min
delDEC_moon23/sighting=-17.5min*0.7352778=-12.9min
DEC_moon/sighting=0deg29.8minS

Ha (Ref.4) = Hs +/- Sextant Error +/- Index Error – Dip = 16deg 12min + 0deg + 0deg + 0deg = 16deg 12min
(Note in this case with the Bubble Horizon, the dip angle and index error are incorporated into the alignment are not considered here).
Ho (Ref.3) = Ha – Refraction +PA +/- SD = 16deg 12min – 3.3min + 57.6min + 0min = 17deg 6.3min
PA = HP*cos(Ha) = 60min * cos(16deg 12min) = 57.6min

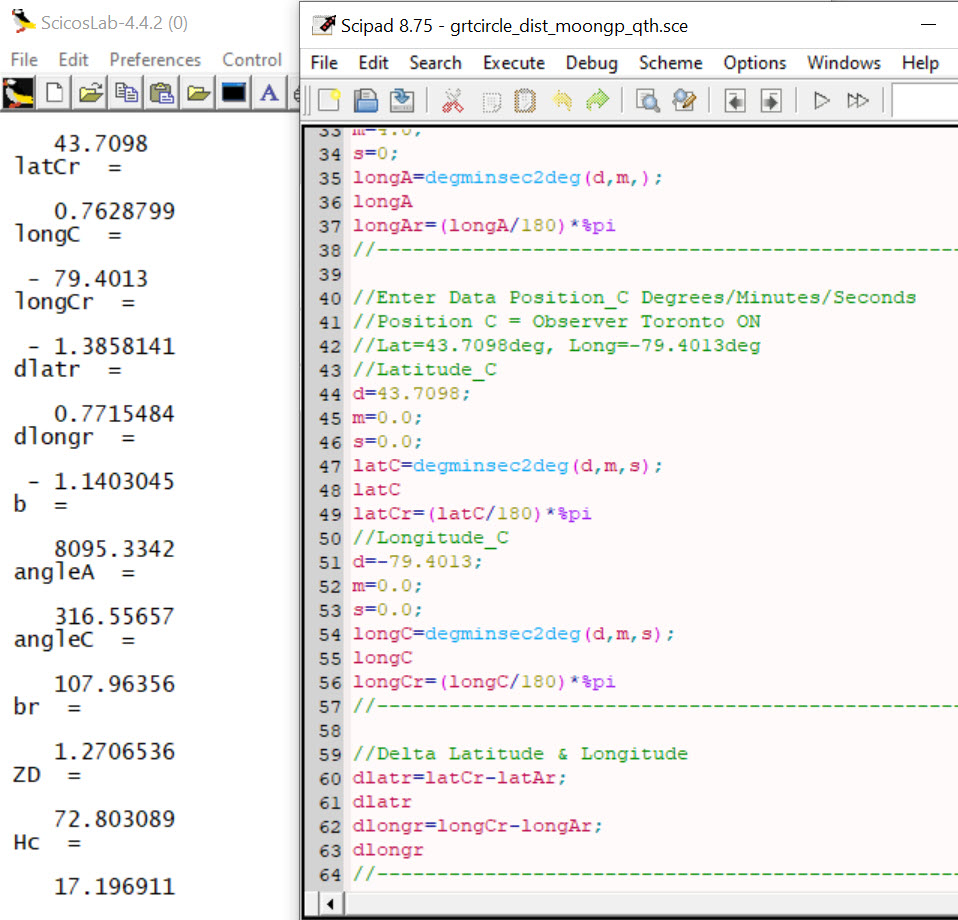
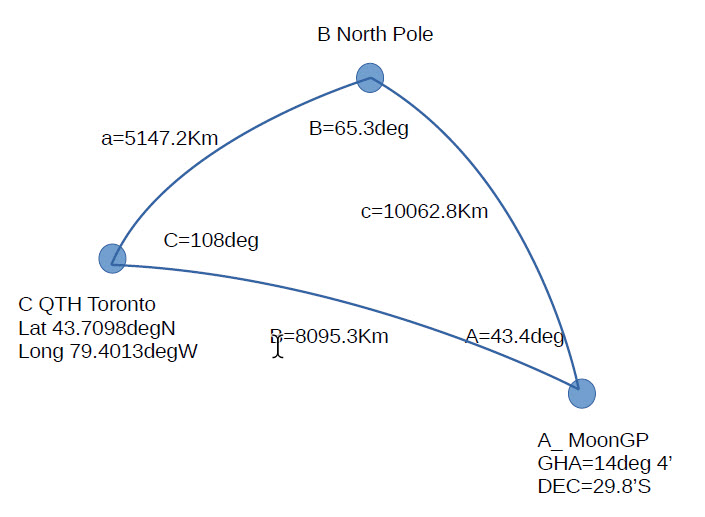
Fig.5 Scicoslab Solution Hc=17deg 11.8min

Since we have the known location of the observer and coordinates of the MoonGP, we can construct the spherical triangle and solve it for hc = 17deg 11.8min as in Figure 5. Rho then follows as Ho-Hc= 17deg 6.3min – 17deg 11.8min = -5.5min